The Limit Comparison Test is a key method in calculus and analysis that allows us to determine if a series converges or diverges. When examining a series of positive terms, like ( \sum a_n ), we can simplify our lives by comparing it with another series ( \sum b_n ) that’s easier to analyze. If the limit
L = \lim_{n \to \infty} \frac{a_n}{b_n}
is a positive finite number, then both series either converge or diverge together. This pivotal idea not only shapes mathematical theory but also finds applications across various fields, including engineering, physics, and finance. So let’s dive deeper into the insights and implications of the Limit Comparison Test—it’s full of surprises!

1. Understanding the Limit Comparison Test
To wrap our heads around the Limit Comparison Test, we must first get specific with the terms involved. Knowing how to analyze and interpret the series you’re working with can change everything. Imagine comparing the harmonic series ( \sum \frac{1}{n} ) with ( \sum \frac{1}{n^{1.1}} ). They show different behaviors—one diverges and the other converges. Thus, understanding the middle part flow of the series you’re comparing is crucial for effectively leveraging the Limit Comparison Test.
You might think of it like making a side-by-side comparison before hitting “purchase” on that new gadget you’ve been eyeing. You want to know how it stacks up. That’s just what the Limit Comparison Test enables you to do its magic—assess how similar or different your series is in its behavior.
Another interesting point is how the Limit Comparison Test streamlines problem-solving in calculus. It allows mathematicians and scientists to identify convergence patterns without needing to dive into intricate calculations, which could ultimately save time and effort. With a well-defined approach, more complex problems become manageable.

2. Top 5 Insights from the Limit Comparison Test
2.1 The Middle Part Flow: Understanding Convergence
The “middle part flow” of comparative series can play a significant role in your outcomes. Let’s break it down with some real examples. When we look at the harmonic series compared to a p-series, we see vital divergence and convergence characteristics. The series ( \sum \frac{1}{n} ) diverges, while ( \sum \frac{1}{n^{1.1}} ) converges. The middle flow determines how we’ll approach convergence testing.
Why does this matter? Well, each series can reveal its behavior through its middle terms, making them valuable in comparative analyses. By understanding those terms, you can leverage the Limit Comparison Test to deliver insights into convergence that might not be immediately evident.
So, taking time to analyze these middle terms not only clarifies your understanding but also fortifies your mathematical toolkit. Think of it as gathering essential GPS updates on your journey through calculus—every little bit can potentially change your direction!
2.2 The Tilt Table Test: A Real-World Application
Here’s where it gets even more relatable! The Tilt Table Test, which is often used in medical fields, provides a useful metaphor for understanding convergence behavior. When you’re evaluating how blood pressure fluctuates in response to tilting, you’re essentially looking at stability or instability—sound familiar?
By applying the same principle to our series, we can view convergence similarly. Just like medical professionals analyze how the body reacts to changes in position, scientists and mathematicians assess their series to understand their properties—laying bare any underlying complexities. This practical analogy makes the test itself even more insightful.
2.3 The Parallel Axis Theorem: Bridging Mechanical and Mathematical Concepts
The Parallel Axis Theorem dives into the details of shifting moments of inertia when considering different axes, and guess what? This concept resonates with the Limit Comparison Test. Just as we observe the shifting moments in mechanics, we need to consider how terms in series behave during shifts.
In practical terms, recognizing these shifts can offer new insights into physical systems. When you apply the theorem alongside the Limit Comparison Test, you gain a richer analytical arsenal, making it easier to connect the dots between mathematical concepts and engineering applications.
2.4 Analyzing the Interchange Map: Visualizing Convergence Patterns
Ever seen an interchange map in play? These visual aids can simplify understanding relationships between series. By graphically representing behaviors, you’ll find it easier to comprehend how different series converge or diverge.
This visual representation helps make sense of seemingly complex data. It lets you see patterns that might otherwise be hidden in numerical crunching. When done effectively, graphical tools can enhance insights drawn from the Limit Comparison Test, highlighting how series interconnect over their domains.
2.5 The Mattress Size Chart: Scale and Dimension in Series
Imagine trying to find the perfect mattress size by sifting through an exhaustive chart—it can be a chore! The same principle applies when comparing series. The idea of “size” becomes crucial just like choosing appropriate dimensions for a comfortable setup.
Consider ( \sum \frac{1}{n^3} ) compared to ( \sum \frac{1}{n^2} ). The former converges and the latter diverges, illustrating that size significantly influences behavior. Knowing how to apply the Limit Comparison Test effectively means understanding these dimensions and how they impact outcomes.
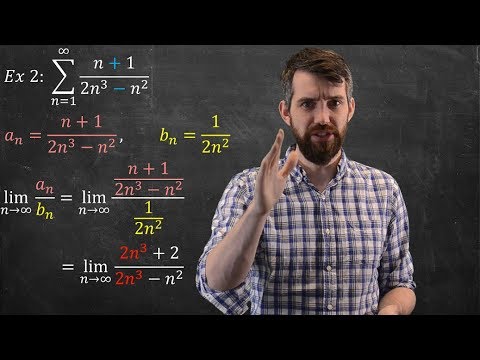
3. The Role of Grip Strengtheners: Enhancing Analytical Capacity
You wouldn’t tackle a heavy lifting session without grip strengtheners, right? Just as these tools enhance your physical prowess, mastering the Limit Comparison Test empowers mathematicians and scientists with an arsenal of analytical skills.
The series convergence tests—various methods and principles—form the backbone of reliable scientific exploration. Embracing them grants professionals the fortitude to address intricate problems with increased confidence and precision, just like crushing that last deadlift.
Think about it—incorporating the Limit Comparison Test into your toolkit isn’t just advantageous; it becomes essential for effective problem-solving in both theoretical and applied mathematics.

4. Center Channel Speaker: Amplifying Observations Through Testing
Picture this: a center channel speaker in your sound system does wonders for amplifying audio clarity. This metaphor resonates perfectly with how the Limit Comparison Test sharpens our understanding of series properties.
Using this test amplifies your focus on convergence behaviors, letting you navigate complicated mathematical principles with greater clarity. It’s like enhancing your audio experience with high-quality sound—everything clicks together seamlessly, enhancing the overall quality!
In conclusion, the Limit Comparison Test transcends being just a procedural tool. It’s a vibrant methodology for exploring the convergence and divergence of series—not to mention its far-reaching applications. This makes it a critical asset for mathematicians, scientists, and professionals at large. As you endeavor to solve complex problems, let this test guide your way, illuminating your path in mathematical analysis!
For deeper explorations of relevant topics, check out related content like the Tilt Table test, real-world applications linked to Brentwood Park, or visual aids inspired by the concepts of Fortnite Memes and their similar interactivity in learning!
Let your understanding and appreciation of series behaviors evolve as you apply the insights gleaned from the Limit Comparison Test!

Limit Comparison Test Insights: Fun Trivia and Interesting Facts
A Snapshot on Convergence Testing
Ever heard about the limit comparison test? It’s a nifty tool in the world of calculus that helps us determine if a series converges or diverges, by looking at its behavior relative to another series. Fascinating, isn’t it? This test can simplify complex scenarios in math, just like finding the best deal on your next big purchase with something like the best buy Citibank offers. You’re comparing two items to the best option available—much like we compare series when analyzing their convergence.
Speaking of comparisons, did you know that the limit comparison test was popularized in the late 19th century? Mathematicians were racing to unlock the mysteries of infinite series, much like the suspenseful twists in the film buried love series Ashes Of regret. This test is not just about numbers but is a triumph of mathematical logic, bridging the gap between simple and complex series in a way that even the most perplexing problems can feel manageable.
Real-Life Applications and Hidden Connections
Another great angle? The limit comparison test isn’t merely a classroom tool; it’s widely applicable in various fields like physics, engineering, and economics! It brings problems down to size, similar to how a lovely meal at Rays Boathouse can transform a dull day into something extraordinary. Just as you might consider the relevance of a film like the lottery ticket movie—where( a young man’s fortunes change thanks to a chance outside luck—here, we give our series the attention they deserve through direct comparison.
Now, if you’re diving into the test, just remember that if two series test a confluence of zero and infinity using real numbers, the results get interesting. Drawing a parallel to gaming, think of how different strategies play out in smite source. Each tactic aligns with unique situations, akin to how various series converge or diverge based on simple limits. It’s all about finding what clicks! The limit comparison test acts as a bridge, so whether you’re mastering an equation or simply living life, it paves the way for clear understanding and insight.